SPSS SLR & MLR

  

SPSS practical (SLR)

Areas    Sales

1726.0  3681.0

1642.0  3895.0

2816.0  6653.0

5555.0  9543.0

1292.0  3418.0

2208.0  5563.0

1313.0  3660.0

1102.0  2694.0

3151.0  5468.0

1516.0  2898.0

5161.0  10674.0

4567.0  7585.0

5841.0  11760.0

3008.0  4085.0

·        First we plot the data as scatter plot

 

                     

·        Then we check correlations between them

Correlations
		area	sales
area	Pearson Correlation	1	.954**
	Sig. (2-tailed)		.000
	N	14	14
sales	Pearson Correlation	.954**	1
	Sig. (2-tailed)	.000
	N	14	14
**. Correlation is significant at the 0.01 level (2-tailed).

 

 

 

 

 

 

 

 Correlation is sig. thus we can develop a linear between sales and area.

 

ANOVAb
Model		Sum of Squares	df	Mean Square	F	Sig.
1	Regression	1.062E8	1	1.062E8	121.009	.000a
	Residual	1.053E7	12	877687.937
	Total	1.167E8	13
a. Predictors: (Constant), area
b. Dependent Variable: sales

Fitted model is sig. significant amount of the variable of the responses (sales) variable has been captured by the fitted model. Sig. amount is given by R²

 

^{·           If the fitted model (SLR) is sig. does 2 parameters are significant???}

                     ^NO

^{corr. is implies model is sig.}

^{model is sig. implies beeta1 is sig.}

^{model is sig. does not implies beeta0 is sig.}

 

Coefficientsa
Model		Unstandardized Coefficients		Standardized Coefficients	t	Sig.
		B	Std. Error	Beta
1	(Constant)	901.247	513.023		1.757	.104
	area	1.686	.153	.954	11.000	.000
a. Dependent Variable: sales

Diagnostics error

Random –DM

Cvonst var –plot of y^hat and error

Normality

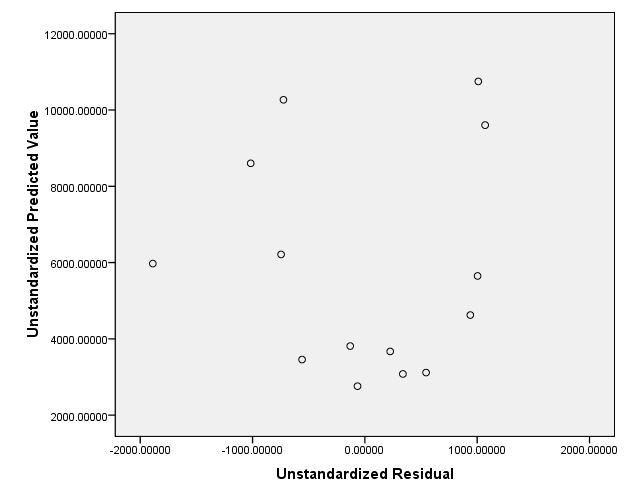
DW statistic is close zero indicating error are random

 

Plot res vs predict indicates random confirming error having constant variance

 

Normality

 

 

Tests of Normality
	Kolmogorov-Smirnova			Shapiro-Wilk
	Statistic	df	Sig.	Statistic	df	Sig.
Unstandardized Residual	.137	14	.200*	.933	14	.333
a. Lilliefors Significance Correction
*. This is a lower bound of the true significance.

SW test stat is not sig. calming the errors are not significant different .

Mean is not sig. diff. from as zero is in 95 % CI .

Can you accept the model??

Percentage error = res*100/obs data

Percentage error varies -46% to 16%

Percentage error varies -19% to 16% with an exceptional one as -46%

 

SPSS practical (MLR)

Y	X1	X2	X3	X4
27	20	50	75	15
23	27	55	60	20
18	22	62	68	16
26	27	55	60	20
23	24	75	72	8
27	30	62	73	18
30	32	79	71	11
23	24	75	72	8
22	22	62	68	16
24	27	55	60	20
16	40	90	78	32
28	32	79	71	11
31	50	84	72	12
22	40	90	78	32
24	20	50	75	15
31	50	84	72	12
29	30	62	73	18
22	27	55	60	20

 

 

Correlations matrix among Y & explanatory variables
		y	x1	x2	x3	x4
y	Pearson Correlation	1	.373	.059	.048	-.522*
	Sig. (2-tailed)		.127	.815	.852	.026
x1	Pearson Correlation	.373	1	.758**	.288	.192
	Sig. (2-tailed)	.127		.000	.247	.444
x2	Pearson Correlation	.059	.758**	1	.555*	.099
	Sig. (2-tailed)	.815	.000		.017	.697
x3	Pearson Correlation	.048	.288	.555*	1	.060
	Sig. (2-tailed)	.852	.247	.017		.813
x4	Pearson Correlation	-.522*	.192	.099	.060	1
	Sig. (2-tailed)	.026	.444	.697	.813
*. Correlation is significant at the 0.05 level (2-tailed).
**. Correlation is significant at the 0.01 level (2-tailed).

Y is sig. corr. only with x4.

Though explanatory variables supposed to be independent, x1 & x2 as well as x2 and x3 are significant.

 

Coefficientsa
Model		Unstandardized Coefficients		Standardized Coefficients	t	Sig.
		B	Std. Error	Beta
1	(Constant)	22.625	7.819		2.894	.013
	x1	.468	.114	1.024	4.112	.001
	x2	-.235	.086	-.777	-2.747	.017
	x3	.156	.134	.224	1.166	.265
	x4	-.407	.098	-.656	-4.150	.001
a. Dependent Variable: y

In SLR model is sig. implies variable is sig.

But MLR model sig. does not implies all variables are sig.

Adding models increases the R², but it does not imply all variable are sig.

Non sig. variables are known nuisance variable.

Prob: how do we decide which parameter to be included in to the model?